
Cornstarch Monster
Summary
Non-Newtonian fluids may behave in unexpected ways. In this demonstration a solution of cornstarch and water creates a "shear thickening" liquid. When placed on a speaker vibrating at low frequency, it appears as though the solution comes alive, growing tentacles and climbing up slopes. IMPORTANT!!! Under no circumstances should an unsupervised minor perform the procedures described herein. All the following described experiments and methods should be supervised by an adult who is completely familiar with and takes full responsibility for all possible hazards.
General Information
Bibliography
- Merkt, et al., “Persistent Holes in a Fluid,” Physical Review Letters, 92 (18), pp. 184501-1 — 84501-4, (2004).
- Ebata, M., Sano, M., “Self-Replicating Holes in a Vertically Vibrated Dense Suspension,” Physical Review Letters, 107, pp. 188301-1 — 188301-4, (2011).
- Gong, et al., “Evolution of the Initial Hole in Vertically Vibrated Shear Thickening Fluids,” Physical Review E, 83, pp. 056311-1 — 056311-9, (2011).
Materials & Methods
 Figure 4: The materials needed for the cornstarch monster.
Figure 4: The materials needed for the cornstarch monster.
You will need the following materials:
- Cornstarch from your local grocery store.
- Water.
- Food coloring (if you prefer a color other than white).
- Speaker. We use a Pyle “Blue Wave” high power 12″ subwoofer (1200 W Max Power), but other subwoofers will work if capable of enough power around 20 Hz.
- An amplifier. We use a “Technical Pro” RX35U amp, capable of 800 W, but others will work.
- Signal generator. We are using an android or apple phone with a signal generation app (Sig Gen), but any signal generator capable of outputting a signal around 20 Hz will do. You could find a free signal generator for your computer simply by searching.
- Plastic sheet to keep the speaker clean. A garbage bag works fine.
Assembling the demonstration:
- Make a solution (about 300 ml) with two parts cornstarch to one part water in a cup. It should be thick enough that the fluid displays non-Newtonian behavior when you stress it (poke it with your finger quickly and it should resist much more than if you poke it slowly).
- If you’d like, add food coloring at this point.
- Connect the speaker to the amplifier’s output and the signal generator to the amplifier’s input according to its manual.
- Place the plastic sheet over the speaker.
- See the procedure section of this module to begin.
Background for Teachers
Like people, different fluids respond to stress in a different ways. Some will flow easily with an applied force, while others will resist. Still others will resist more and more with increasing stress, and their counterparts will eventually give in to increasing stress.
NEWTONIAN FLUIDS
Many of the fluids we interact with are called Newtonian fluids, as their behavior was initially described by Sir Isaac Newton. These fluids experience a stress that is linearly proportional to the rate of strain placed on them:
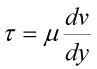
In other words, the shear stress, 𝝉, in the water equals a constant viscosity, μ, multiplied by the change in velocity, v, in the fluid in the direction of the shear, y. Viscosity is a measure of how resistant to flow the fluid is. Water, for example, has a low viscosity compared to honey.
To understand the relationship between stress and shear rate, consider swimming. As your hand moves through the water, it experiences an opposing force caused by friction with the water, a drag force. As you pull the water adjacent to your hand along at the speed of your hand, that water also pulls along the water adjacent to it, causing it to move, though at a speed slightly slower than your hand. You end up creating a gradient of fluid velocity from the speed of your hand at its surface, to zero far away from your hand. This gradient of velocity creates shear stresses as adjacent flows of water accelerate or decelerate their neighbors. The resulting force is translated to your hand and that is the force that propels you.
Because water is a Newtonian fluid, these shear stresses are proportional to the shear rate. The faster you move your hand, the velocity gradient becomes steeper, and you’ll experience a greater drag force on your hand (and swim faster). If you were swimming in a more viscous fluid, such as honey, you would get more propelling force for a given velocity of your hand (though you’d also encounter more force opposing the forward movement of your body through the fluid).
NON-NEWTONIAN FLUIDS
For non-newtonian fluids, the apparent viscosity in Equation 1 is a function of the velocity gradient, and there are several types of non-newtonian fluids. Some are shear-thinning (pseudoplastics); for these fluids, the viscosity decreases with greater shear rates. An example of such a fluid would be blood, or ketchup. These fluids are relatively viscous, or thick, when they experience low velocity gradients, but become more amenable to flow once they are in motion. A fluid such as ketchup, or mayonnaise is also what we call a Bingham plastic, in that it takes a certain level of stress before the fluid will flow at all; otherwise it acts as a solid, retaining its shape (and clinging to the side of the mayonnaise jar).
DELATANT FLUIDS
The type of fluid we are using in this module is a corn startch solution and it falls on the other side of the spectrum of non-newtonian fluids. This is a shear-thickening (or delatant) fluid, in that its viscosity increases as the shear rate increases. If you, say, flow this type of fluid slowly through a tube, it will move with relatively little resistance, but if you try to flow it at a high velocity, high velocity gradients will develop, and it will quickly become energy intensive to keep the fluid moving.
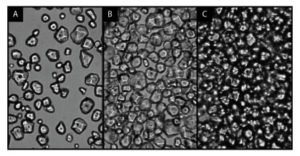
Figure 2: Cornstarch under the microscope at various concentrations.
The reason for this behavior may be seen in the makeup of cornstarch solutions. These solutions are actually suspensions of solid particles in water. Figure 2 shows our fluid at various concentrations of cornstarch in water (Figure 2C is the concentration used in the cornstarch monster). As you can see in Figure 2A, cornstarch powder is made up of many solid grains of starch. When these grains become packed tightly together, as they are in Figure 2C, they may have two primary responses to shear rate. At low shear rate, the grains may act individually and flow around each other relatively easily, as they are lubricated by the surrounding water. However, if we apply a high shear on this solution, the solid particles begin to aggregate and lock up against their neighbors before they can make their way around each other. Like groups of people walking on a busy street in different direction, they may negotiate around each other if given enough time to redirect themselves to avoid oncoming traffic, but travel will become much more difficult if the crowds begin to hold hands and run against each other blindly.
VIBRATING CORNSTARCH SOLUTIONS
When placed on a vibrating speaker, the cornstarch fluid is rapidly accelerated up and down with the speaker cone. At low amplitudes and at about 20 Hz Faraday waves develop on the liquid’s surface, which are well-understood standing waves of sound. This sound reflects around the solution and areas of constructive and destructive interference cause the solution to bulge and dip slightly in a some pattern.
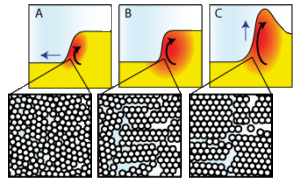
Figure 3: Theory behind the cornstarch monster. Cornstarch is shown as yellow with relatively high viscosity areas in red. Each image shows the area around a discontinuity in fluid height and an hypothesized structure of the cornstarch grains at each condition. A) Low speaker amplitude, when the fluid flows to relax the height discontinuity. B) A medium, critical amplitude, where convection perfectly counteracts hydrodynamic forces. C) A high, super-critical amplitude, where vertical fingers form.
The physics become more complicated and not as well understood if we increase the amplitude and introduce a slight discontinuity in the fluid’s surface. We do this by pulling the solution off the center of the speaker, thereby making a difference in height between adjacent areas of the solution, but others create a hole in the solution by blowing air on to it. At low acceleration of the fluid (at low speaker volume) a small convection current is created at the edge of the height difference, according to Reference 4 in our Bibliography, but this reference is not clear how convection may occur here (I will attempt to give my take on it below, but all of this should be taken with a grain of salt). The viscosity remains low and the grains of the cornstarch closely pack and flow around each other (Figure 3A). This convention-like flow is not large enough, at such low acceleration, to counteract the hydrodynamic pressure caused by the difference in height, and so the hole eventually fills in, as you would expect for a Newtonian fluid.
As acceleration increases with increasing sound amplitude (Figure 3B) shear stresses at the height discontinuity increase, causing the grains to aggregate and make the fluid more viscous. As the vibrations increase this convection-like flow also increases to the point where it counteracts the flow that would be caused by hydrodynamic pressure. In this case the hole may remain open for a long while, as is observed experimentally.
As acceleration increases even further (Figure 3C) shear stresses increase more, causing the grains to aggregate even more and greatly increase the local apparent viscosity. The convection-like flow increases to the point that abnormally viscous fluid begins to pile up at the border and form fingers that grow and eventually fall over under the force of gravity. Once they fall into the solution they create more height discontinuities which then may lead to more fingers, and give birth to the writhing cornstarch monster.
As stated above, the reasons behind the flow at the edge of these height discontinuities remain vague in published journal articles. Some articles point to this question as one that remains unanswered. So how does it happen?
I’m really not certain either, but I’ll give it a completely informal guess.
It seems there are a couple factors that lead to a hysteresis in the cyclic acceleration of the fluid caused by the speaker’s vibration (acceleration up is not the same as acceleration down at the discontinuity). Firstly, when the fluid is accelerated up, by the push of the speaker, it also experiences the acceleration due to gravity as an additive acceleration. The force of gravity adds to the force from the speaker. When the fluid is accelerated down by the speaker, gravity acts to relieve that force. Secondly, when the solution is accelerated down, it is restricted by the solid barrier of the speaker cone; whereas it is not similarly restricted by the air-cornstarch fluid interface when accelerated up.
At height discontinuities, there is a vertical interface between the cornstarch solution and the air, causing a sharp discontinuity in viscosity, which allow the cornstarch at this boundary to move more quickly up and down than the fluid in the bulk. This greater flow leads to the development of the largest change in solution velocities across the horizontal axis near this vertical interface, and because this is a delatant fluid, that means a sharp increase in viscosity at this boundary. As the speaker pushes up at this interface, the viscosity of the fluid near the interface becomes relatively large and the solution becomes thicker, more viscous, and this plug of firmer fluid may move higher than the rest of the fluid, having one boundary open to air, which is far less viscous. As this plug moves up, less viscous fluid from the bulk may flow in to take its place.
When the fluid accelerates down, the velocity gradient is diminished and so the solution is less thick, but, more importantly, the fluid all across the interface with the speaker retains the shape of the speaker; it cannot form a “finger” pointing down. Therefore, it seems possible that each time the solution moves up, it pushes up a relatively firm plug of thick delatant solution, and through the cycle the less viscous solution further away from the height discontinuity can move in below the plug. When the fluid is accelerated down, the less viscous solution that took the plug’s place now undergoes elevated stress and itself becomes more viscous. The fluid in the finger cannot flow fast enough to go back to where it was before the system begins to accelerate up again. Once a finger starts, it has high shear all around it, and thereby grows and remains thick until it falls over.
Again, take the above with skepticism, as even the last paper I found published on this topic in 2011 seems uncertain as to what is physically going on and this is just my intuition.
Instructional Procedures
- If you haven’t already done so, mix the cornstarch solution as described in the materials section of this module.
- Allow the students to touch the solution. Note how the solution responds to both slow and quick movements.
- Pour the cornstarch solution on to the plastic, in the middle of the speaker.
- Turn the volume on the amplifier all the way down and then start the signal generator with a 20 Hz sinusoidal signal.
- Turn up the volume on the amplifier until the solution begins to vibrate.
- If tentacles do not form, pull on the plastic to move the cornstarch off center. If that does not work you may need to turn up the volume or adjust the frequency (Between 18 and 25 Hz seems to work best for us). You may also try altering the solution recipe.
- Let each student observe the “monster”.
- Turn the volume down and the solution should relax into a puddle.
- You can keep the solution for a day or two if you keep the water from evaporating, and remix the solution before each use. However, it will soon be colonized my microbes.